Fra 'Signature in the cell' kap 9-10: Kunne liv oppstått tilfeldig?

 (S.C.Meyer; Harper One)

Alt levende består av proteiner. Proteiner bygges opp av aminosyrer. Det å bygge en fungerende celle, noe á la det vi kjenner i dag, ville selvsagt krevd mer enn den genetiske informajonen som styrer protein-syntesen. Det ville også krevd medfølgende preeksistente proteiner og RNA-molekyler, tRNAs, mRNAs etc for å prosessere og tyde informasjonen lagret i DNA. Det er faktisk over 100 spesifikke proteiner involvert i enkle bakterielle oversetter-systemer, ca 20 flere er involvert i transkripsjon og over 30 i DNA-replikasjon. Så selv om proteiner er avhengige av DNA, er mange proteiner avhengige for tydningen og prosessering av info i DNA.

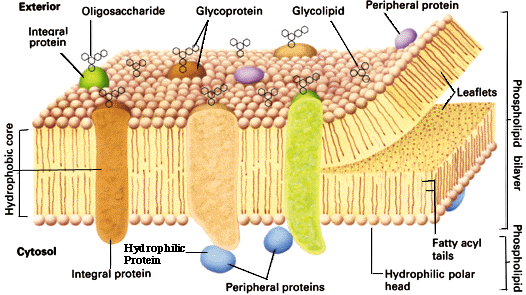Foruten dette, måtte den første cellen ha krevd en slags halvt-gjennomtrengelig membran og en cellevegg for å beskytte seg og de kjemiske reaksjonene i den. En clik membran er i moderne bakterier laget av proteiner og enzymer som linker seg sammen. Celler krever en rekke av små molekyler i form av sukker, vitaminer, metaller, fosfater, mineraler og ATP i tillegg til proteiner og etc. Det integrerte systemet vanskeliggjør en beregning av sannsynligheten, og gjør at den sannsynligvis underestimeres grovt.

For å kalkulere en sannsynlighet for at liv skal oppstå tilfeldig, bruker man en litt indirekte metode. En kalkulerer først sannsynligheten for at ett enkelt, fungerende protein av gjennomsnittlig lengde skal oppstå ved tilfeldighet alene. Så multiplisereren en, som ved uavhengige begivenheter med sannsynligheten for at hver av de andre proteinene oppstår ved tilfeldighet. Det er litt lettere å beregne sjansen for at proteinene skal komme sammen ved tilfeldighet, enn for genene , så derfor gjør de fleste det.

Vi forutsetter for enkelhets skyld et enkelt protein på 150 aminosyrer. I en kjede på 150 aminosyrer er 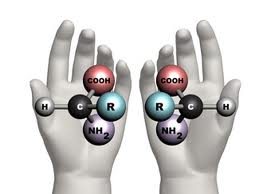sekvensen på disse sentral, for at det skal bli et fungerende protein. Om en tar utgangspunkt i ett spesifikt protein, så er det for hver av de 150 plasseringene 20 mulige aminosyrer å velge mellom. Det innebærer at for hele proteinet så vil det være 20 opphøyd i 150 mulige kombinasjoner: 1,4*10 opphøyd i 195. For å finne muligheten for at et hvilket som helst protein skal dannes tilfeldig, må en ta høyde for at det er flere mulige kombinasjoner av aminorsyrer som kan gjøre ett spesifikt protein funksjonsdyktig. Gjør en dette, kommer en ned på en sannsynlighet 1: 10 opphøyd i 74 (iflg. Douglas Axe).
Problemet er at aminosyrene har både og D-og L-form (symmetriske) ute i naturen, mens i levende organismer finnes bare L-formen. I tillegg forekommer det også to slags bindinger mellom aminosyrer: peptid og ikke-peptid bindinger. Begge disse forekommer i ca like blandinger (50/50). Det er ikke 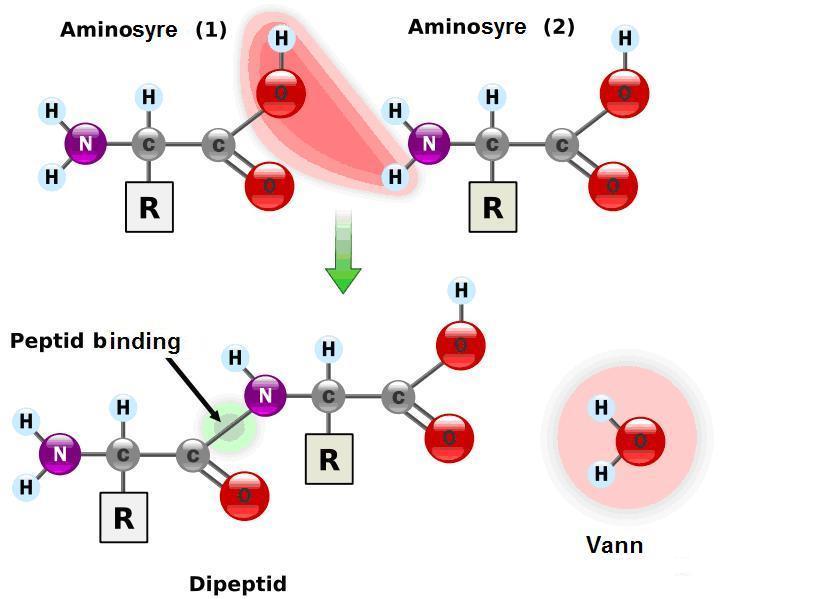kjemiske forhold som gjør hvorvidt en D- eller L-formet aminosyre lenker seg til en annen. Det samme gjelder angående peptid-bindinger. Sannsynligheten for begge typer kan dermed røft settes til 1/2. Sannsynlighten for at begge disse tilfeldig skal lenke seg sammen for 150 aminosyrer blir da: (1/2) opphøyd i 300 (150+150). Denne sannsynligheten er ca 5*10opphøyd i (-91). Multipliserer vi disse er vi på størrelsesorden: 10 opphøyd i (-165)

Endelig er det nødvendig med et helt sett proteiner for å få en fungerende celle. Vi vil holde oss til et lavt tall: 250. Det finnes dem som har anslått et betydelig lavere tall, men de har ikke dokumentert noe angående dette. Om en tar hensyn til dette, multipliserer sannsynlighetene, kommer en til en sannsynlighet for at en enkelt slik begivenhet skal inntreffe på 1:10 opphøyd i ca 41000. Dette er et tall meget nær null. Ja, det er så nær null at matematikere vil benekte at en begivenhet med en slik sannsynlighet noensinn vil oppstå. Men hva er så det gunstige utfallsrommet?

Igjen er det mye avhengig av forutsetninger og hvor vide disse gjøres. Vi forutsetter med Dembski at det eksisterer ca 10 opphøyd i 80 elementærpartikler i det observerbare univers. Da Demski regnet på dette, fant han at det da var gått ca (10 opphøyd i 16) sekunder siden the Big Bang (ca 13,7 milliarder år). Når en skal ta i betraktning hvor ofte slike elmentærpartikler kan reagere med hverandre, så er den en nedre skranke en ikke kan underskride. Det er en såkalt Planck-lengde (10 opphøyd i -33 cm). Tiden lyset bruker på en dette, tilsvarer 10 opphøyd i -43 sekunder. Altså er det i prinsippet mulig, med 10 opphøyd i 43 reaksjoner pr sekund. Om en skal se hvor mange partikler som kan reagere med hverandre til enhver tid, så ville det antagelig være bare 1 promille som kunne reagere med hverandre samtidig. Men for å være romslige regner vi det som alle kan det. Antall gunstige utfallsrom blir da 10 opphøyd i (80+16+43). Det tilsvarer anslagsvis 10 opphøyd i 140. Dette er et meget stort tall, men sammenlignet med mulig utfallsrom på 10 opphøyd i ca 41000, blir det en sannsynlighet på 10 opphøyd i (-40860).

Omgivelses faktorer

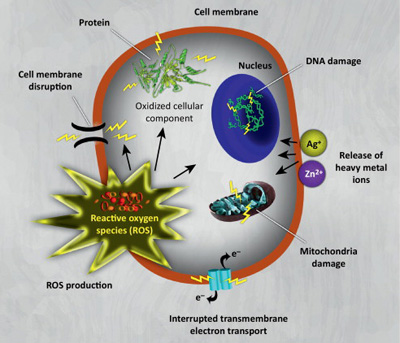Nå hviler disse beregningene på forutsetninger om at det fantes en slags pre-biotisk suppe, bestående av mye Nitrogen. Nå viser det seg at Nitrogen nivået til pre-Cambrium var lav, mindre enn 0,15%. Ut fra dette, kan vi slutte at det ikke fantes en slik pre-biologisk suppe. Om den skulle ha eksistert, ville det vært kun for en kort periode. Det ville gjøre resultatet enda mindre sannsynlig. Beregningene ovenfor gjelder gitt at et såkalt 'best-case' estimat av de relevante ressursene for begivenheten eksisterer.
Nå er det slik at en celle bygges opp av mange informasjonsrike molekyler. Men for at endog en eneste av disse skulle oppstå tilfeldig, er en sjanse på en billiontedels biliondel. Så ville også omgivelsen være fiendtlige for molekyler av aminosyrer. Mens en tidligere ikke trodde oksygen fantes i særlige mengder, har en kommet til at oksygen fantes endog før planteliv. Oksygen ville fungere som gift for proteiner under oppbygning..

Men til tross for disse ødeleggende resultatene, for tilhengere av at liv kunne oppstå tilfeldig, har de prøvd øke sjansen ved enten å redusere kravet til kompleksitet eller ved å øke det gunstige utfallsrommet. De foreslår en kombinasjon av lovmessighet og sjanse, fra et selv-replikerende molekyl fantes. Likeså vil de øke det gunstige utfallsrommet ved å postulere eksistensen av flere parallelle multivers, et høyst spekulativt foretagende. Men hva gjør en ikke for å kunne unngår muligheten av ett designet univers? Vi kommer tilbake til begge disse 'fluktrutene' på min blogg -på et senere tidspunkt.